Проверка гипотезы основана на статистическом анализе. Статистическая значимость вычисляется с использованием p-значения, которое сообщает вам, насколько вероятно, что ваш результат будет иметь место, учитывая, что конкретное утверждение (нулевая гипотеза) верно. Если это значение p меньше уровня значимости (обычно 0,05), то экспериментатор может предположить, что нулевая гипотеза ложна и что альтернативная гипотеза принята. Используя простой t-критерий, вы можете вычислить p-значение и определить значимость между двумя разными группами данных.
метод
Часть 1 из 3. Создайте свой эксперимент

Шаг 1. Определите свою гипотезу
Первым шагом в оценке статистической значимости является определение вопроса, на который вы хотите ответить, и выдвижение своей гипотезы. Гипотеза - это утверждение о ваших экспериментальных данных и возможных различиях в популяции. Каждый эксперимент имеет нулевую и альтернативную гипотезы, и обычно вы сравниваете две группы, чтобы увидеть, совпадают они или нет.
- Нулевая гипотеза (H0) обычно утверждает, что между вашими двумя наборами данных нет никакой разницы. Например: учащиеся, прочитавшие материал до начала курса, не получают более высоких оценок.
- Альтернативная гипотеза (Ha) противоположна нулевой гипотезе и, следовательно, утверждению, которое вы хотите подтвердить своими экспериментальными данными. Например: учащиеся, прочитавшие материал до начала курса, получают лучшие итоговые оценки.

Шаг 2. Определите уровень значимости, чтобы определить, насколько необычными должны быть ваши данные, чтобы их можно было считать значимыми
Уровень значимости (также называемый альфа) - это порог, который вы устанавливаете для определения значимости. Если ваше p-значение меньше или равно уровню значимости, то данные считаются статистически значимыми.
- Как правило, уровень значимости (или альфа) часто устанавливается равным 0,05, что означает, что вероятность случайного наблюдения различий в ваших данных составляет всего 5%.
- Более высокий уровень достоверности (и, следовательно, более низкое значение p) означает, что результаты более значимы.
- Если вам нужна более высокая степень уверенности в своих данных, установите значение p ниже 0,01. Более низкие значения p часто используются на производстве, когда дело доходит до обнаружения дефектов в продуктах. Очень важно иметь высокий уровень уверенности в том, что каждая деталь будет работать именно так, как должна.
- Для большинства экспериментов, основанных на гипотезах, приемлем уровень значимости 0,05.
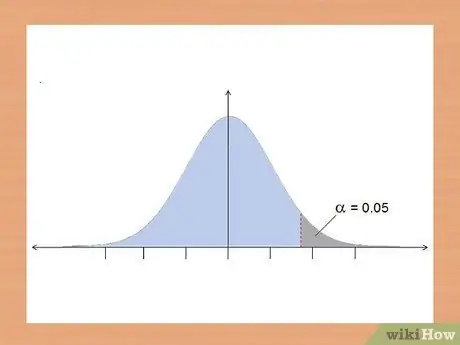
Шаг 3. Решите, хотите ли вы использовать односторонний или двусторонний тест
Одно из предположений в t-тесте состоит в том, что ваши данные распределены нормально. Нормальное распределение данных образует колоколообразную кривую, при этом большая часть данных попадает в середину. T-тест - это математический тест, чтобы увидеть, находятся ли ваши данные за пределами нормального распределения - выше или ниже на концах кривой.
- Если вы не уверены, будут ли ваши данные выше или ниже контрольной группы, используйте двусторонний тест. Это позволяет проверить значимость в обоих направлениях.
- Как только вы узнаете, куда могут направиться ваши данные, используйте односторонний тест. В нашем примере вы ожидаете, что оценки учащихся улучшатся, поэтому вы должны использовать односторонний тест.
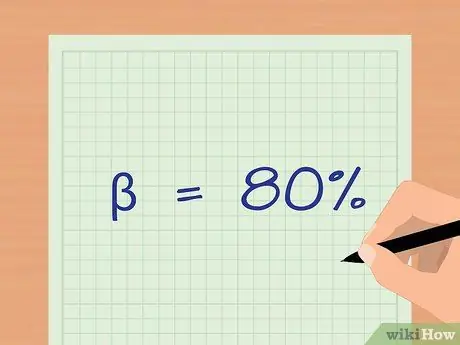
Шаг 4. Определите размер выборки с помощью анализа производительности
Производительность теста - это вероятность того, что ожидаемый результат будет получен при заданном размере выборки. Обычный предел производительности (или ß) составляет 80%. Анализ производительности может быть немного сложным без некоторых начальных данных, потому что вам нужны некоторые данные об ожидаемых средних значениях каждой группы и их стандартных отклонениях. Используйте онлайн-калькулятор анализа производительности, чтобы определить оптимальный размер выборки для ваших данных.
- Ученые обычно проводят небольшое пилотное исследование, чтобы получить информацию для анализа эффективности и определить размер выборки для более крупного и всестороннего исследования.
- Если у вас нет ресурсов для проведения сложного пилотного исследования, сделайте некоторые оценки возможных средств. Вы можете основывать это на чтении специальной литературы и подобных исследованиях, которые уже проводились. Это дает вам хорошую отправную точку для размера вашей выборки.
Часть 2 из 3. Рассчитайте стандартное отклонение
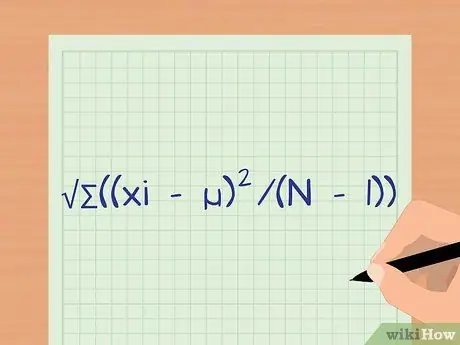
Шаг 1. Определите формулу для стандартного отклонения
Стандартное отклонение показывает, как распределяются ваши данные. Он дает вам информацию о том, насколько похожи каждая точка данных в вашей выборке. На первый взгляд уравнение может показаться немного сложным, но в следующих шагах мы проведем вас через построение расчета. Формула s = √∑ ((xi -µ) 2 / (N - 1)).
- s - стандартное отклонение.
- Означает, что вы просуммируете все собранные вами выборочные значения.
- xi представляет каждое отдельное значение ваших данных.
- µ - это среднее значение ваших данных для каждой группы.
- N - общее количество выборок.

Шаг 2. Возьмите среднее значение образцов для каждой группы
Чтобы рассчитать стандартное отклонение, вы должны сначала взять среднее значение образцов в каждой группе. Среднее значение обозначается греческой буквой Mu или µ. Для этого вы просто складываете все отдельные сэмплы, а затем делите их на общее количество сэмплов.
- Например, чтобы узнать среднюю оценку группы, прочитавшей материал перед уроком, мы смотрим на данные. Для простоты мы будем использовать набор данных из 5 точек: 90, 91, 83, 85 и 94.
- Сложите все образцы: 90 + 91 + 85 + 83 + 94 = 443.
- Разделите сумму на количество образцов, N = 5: 443/5 = 88,6.
- Средняя оценка по этой группе - 88,6.

Шаг 3. Вычтите каждый образец из среднего
Следующая часть расчета включает (xi - µ) часть уравнения. Вы вычтите каждую выборку из только что рассчитанного вами среднего значения. В нашем примере вы получите пять вычитаний.
- (90-88, 6), (91-88, 6), (85-88, 6), (83-88, 6) и (94-88, 6).
- Рассчитанные числа теперь 1, 4; 2, 4; -3, 6; 5, 6 и 5, 4.

Шаг 4. Возведите в квадрат каждое из этих чисел и сложите их
Теперь каждое из новых чисел, которые вы только что рассчитали, будет возведено в квадрат. Этот шаг также устраняет все негативные признаки. Если после этого шага или в конце расчета у вас стоит знак минуса, возможно, вы пропустили этот шаг.
- В нашем примере мы теперь работаем с 1.96; 5, 76; 12,96; 31, 36 и 29, 16.
- Если сложить эти квадраты, мы получим: 1, 96 + 5, 76 + 12,96 + 31,36 + 29, 16 = 81, 2.
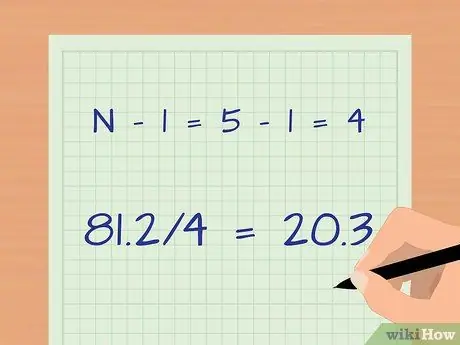
Шаг 5. Разделите на общее количество образцов минус 1
Формула делится на N - 1, потому что она исправляет тот факт, что вы не подсчитали всю совокупность - вы берете выборку из всех учащихся, чтобы получить оценку.
- Вычтем: N - 1 = 5-1 = 4
- Разделить: 81, 2/4 = 20, 3
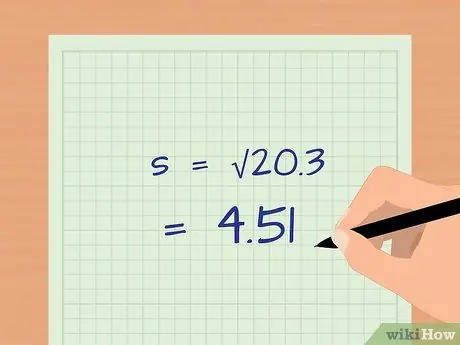
Шаг 6. Извлеките квадратный корень
Разделив число выборки минус 1, вы извлечете квадратный корень из этого окончательного числа. Это последний шаг в вычислении стандартного отклонения. Существуют статистические программы, которые делают этот расчет за вас после того, как вы ввели необработанные данные.
В нашем примере стандартное отклонение итоговых оценок учащихся, читающих перед уроком, составляет: s = √20,3 = 4,51
Часть 3 из 3: определение значимости

Шаг 1. Рассчитайте разницу между двумя вашими учебными группами
До сих пор наш пример касался только одной из исследовательских групп. Конечно, если вы хотите сравнить две группы, вам нужны данные из обеих. Рассчитайте стандартное отклонение для второй исследовательской группы и используйте его для определения дисперсии между двумя исследовательскими группами. Формула дисперсии: sd = √ ((s1 / n1) + (s2 / n2))
- SD - это разница между вашими группами.
- s1 - стандартное отклонение группы 1, а N1 - размер выборки группы 1.
- s2 - стандартное отклонение группы 2, а N2 - размер выборки группы 2.
-
В нашем примере предположим, что данные из группы 2 (студенты, которые не читали перед уроком) имели размер выборки 5 и стандартное отклонение 5,81. Дисперсия составляет:
- sd = √ ((s1) 2 / N1) + ((s2) 2 / N2))
- sd = √ (((4, 51) 2/5) + ((5, 81) 2/5)) = √ ((20, 34/5) + (33, 76/5)) = √ (4, 07 + 6, 75) = √10, 82 = 3, 29.

Шаг 2. Рассчитайте t-значение ваших данных
Значение t помещает ваши данные в форму, позволяющую сравнивать их с другими данными. Используя t-значения, вы можете выполнить t-тест, с помощью которого вы можете вычислить вероятность того, что две группы значительно отличаются друг от друга. Формула для значения t: t = (µ1 - µ2) / sd.
- µ1 - среднее значение первой группы.
- µ2 - среднее значение второй группы.
- sd - это разница между вашими выборками.
- Используйте среднее значение больше, чем µ1, чтобы не получить отрицательное значение t.
- В нашем примере мы говорим, что среднее значение для группы 2 (тех, кто не читал) было 80. Значение t: t = (µ1 - µ2) / sd = (88, 6 - 80) / 3, 29 = 2.61.
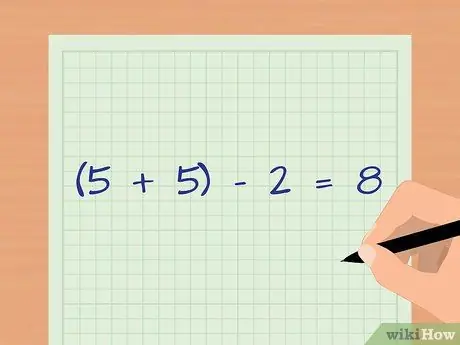
Шаг 3. Определите степени свободы вашего образца
При расчете с использованием t-значения количество степеней свободы определяется размером исследовательской группы. Суммируйте количество образцов из каждой группы, затем вычтите два. В нашем примере степени свободы равны 8, потому что в первой группе пять образцов, а во второй - пять (5 + 5) - 2 = 8).

Шаг 4. Используйте t-таблицу для оценки значимости
Вы можете найти таблицу с t-значениями и степенями свободы в стандартной работе по статистике или в Интернете. Посмотрите на строку, содержащую степени свободы для ваших данных, и найдите p-значение, соответствующее вашему t-значению.
При 8 степенях свободы и значении t 2,61 значение p для одностороннего теста будет находиться в диапазоне от 0,01 до 0,025. Поскольку мы устанавливаем наш уровень значимости меньше или равным 0,05, наши данные статистически значимы. Имея эти данные, мы отвергаем нулевую гипотезу и принимаем альтернативную гипотезу: учащиеся, читающие перед уроком, получают лучшие итоговые оценки

Шаг 5. Рассмотрите возможность последующего исследования
Многие ученые проводят небольшое пилотное исследование с несколькими чтениями, чтобы лучше понять, как они могут провести более крупное исследование. Если вы проведете еще одно исследование с большим количеством измерений, вы будете больше уверены в своем заключении.
