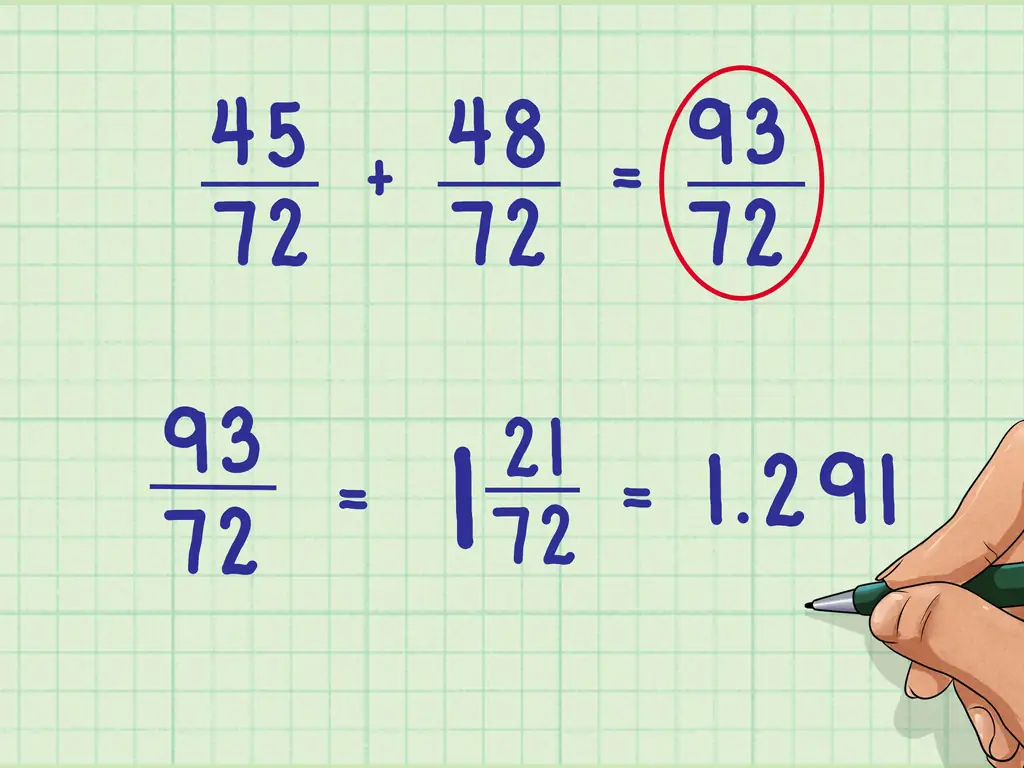Дробь состоит из числителя и знаменателя. Когда две дроби имеют одинаковый знаменатель, они считаются общими. Сложить дроби с общим знаменателем просто, достаточно сложить числители! Новая дробь будет использовать тот же первоначальный знаменатель, поэтому вам нужно беспокоиться только о верхнем числе. То же самое и с операцией вычитания. Ситуация немного усложняется, когда дроби имеют разный знаменатель, но их все равно можно складывать или вычитать, сначала найдя общий знаменатель.
шаги
Часть 1 из 3: сложение дробей с общими знаменателями

Шаг 1. Узнайте числитель и знаменатель
Дробь состоит из двух частей: числителя (число вверху делительной линии) и знаменателя (число внизу). В то время как знаменатель указывает, на сколько частей было разделено целое число, числитель указывает, сколько частей целого числа.
Например, в дроби ½ числитель = 1, а знаменатель = 2, то есть дробь равна половине

Шаг 2. Определите знаменатель
Когда две или более дробей имеют общий знаменатель, это означает, что они имеют одинаковое число в знаменателе или что все они представляют собой целые меры, разделенные на одинаковое количество частей. Дроби с общим знаменателем можно легко сложить вместе, и полученная дробь будет иметь тот же знаменатель, что и исходные дроби. Например:
- Дроби 3/5 и 2/5 имеют общий знаменатель 5.
- Дроби 3/8, 5/8 и 17/8 имеют общий знаменатель 8.

Шаг 3. Найдите числители
Чтобы сложить дроби с общим знаменателем, просто сложите числители и перепишите сумму поверх исходного общего знаменателя.
- В дробях 3/5 и 2/5 числители 3 и 2.
- В дробях 3/8, 5/8 и 17/8 числители 3, 5 и 17.
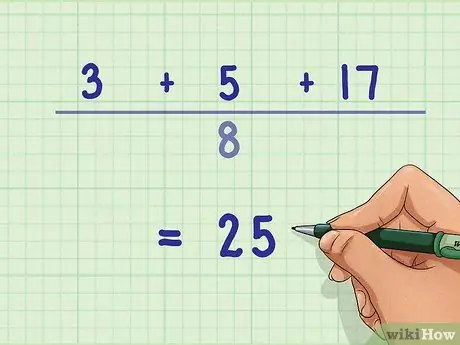
Шаг 4. Сложите числители
В примере 3/5 + 2/5 сложите числители 3 + 2 = 5. В примере 3/8 + 5/8 + 17/8 сложите числители 3 + 5 + 17 = 25.
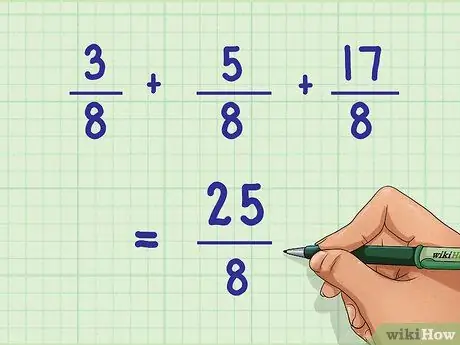
Шаг 5. Перепишите дробь с новым числителем
Не забудьте использовать общий знаменатель, так как количество частей, на которые делится целое число, остается неизменным, и вы просто складываете количество отдельных частей.
- Дроби 3/5 + 2/5 = 5/5
- Дроби 3/8 + 5/8 + 17/8 = 25/8
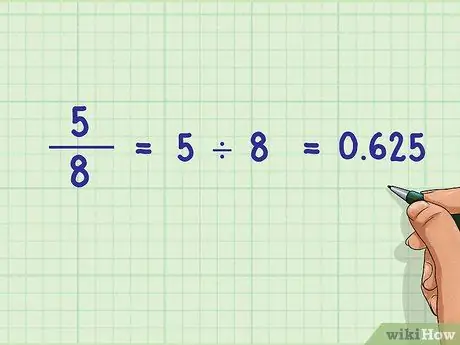
Шаг 6. Решите дробь, если необходимо
Иногда дробь можно упростить, включая ее деление для получения целого числа (а не дроби или десятичной дроби). В примере 5/5 эту дробь можно легко решить, так как любая дробь, в которой числитель равен числителю, дает число 1. Думайте об этом как о круге, разделенном на три части. Когда вы съедаете три куска пиццы, вы съедаете целую пиццу.
Любую дробь можно преобразовать, разделив числитель на знаменатель, и вы обычно получаете десятичное число. Например, 5/8 также можно записать как 5 ÷ 8, что равно 0,625
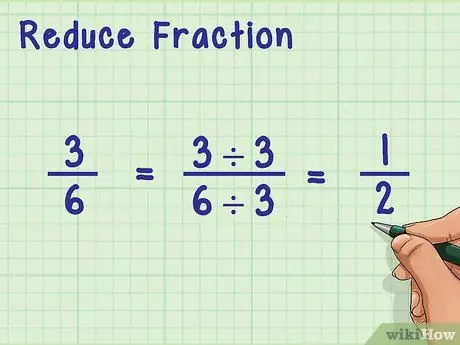
Шаг 7. По возможности уменьшите фракцию
Дробь имеет простейшую форму, когда числитель и знаменатель не имеют общего множителя, на который их можно разделить.
Например, в дроби 3/6 и числитель, и знаменатель имеют общий множитель 3, то есть оба могут быть разделены на 3 для получения целого числа. Следовательно, дробь 3/6 можно рассматривать как 3 ÷ 3/6 ÷ 3 = ½
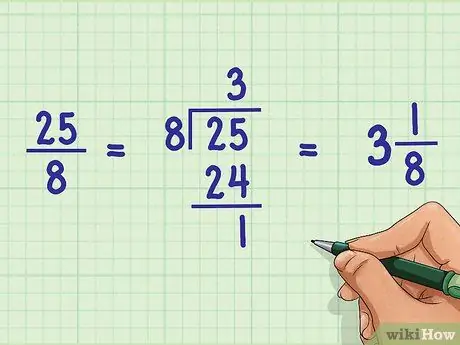
Шаг 8. Преобразуйте неправильные дроби в смешанные числа, если необходимо
Если числитель дроби больше ее знаменателя, например 25/8, это называется неправильной дробью (когда происходит обратное, это правильная дробь). Их можно преобразовать в смешанное число, то есть целое число плюс его собственная дробь. Чтобы преобразовать неправильную дробь 25/8 в смешанное число, выполните следующие действия:
- Разделите числитель неправильной дроби на ее знаменатель, чтобы определить, сколько раз число 8 умещается в числе 25, то есть 25 ÷ 8 = 3 (, 125)
- Остальное определите. Если 8 x 3 = 24, вычтите это значение из исходного числителя: 25-24 = 1, где разница - это новый числитель.
- Перепишите смешанное число. Знаменатель будет равен исходной неправильной дроби, т.е. 25/8 можно заменить на 3 1/8.
Часть 2 из 3: Вычитание дробей с общими знаменателями

Шаг 1. Найдите числители и знаменатели
Например, см. Уравнение 12/26 - 4/26 - 1/26. В этом примере:
- В числителях 12, 4 и 1.
- Общий знаменатель 26.

Шаг 2. Вычтите числители
Как и в случае с сложением, вам не нужно беспокоиться о знаменателе, поэтому просто найдите разницу между числителями:
- 12 - 4 - 1 = 7
- Запишите дробь с новым числителем. 26.12 - 26.04 - 26.01 = 26.07.
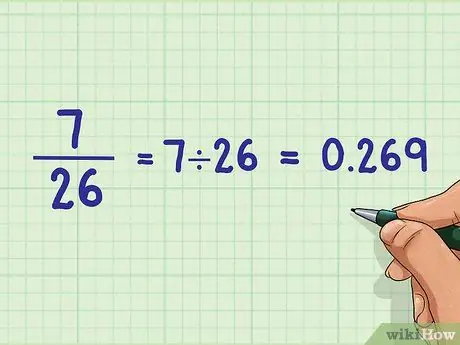
Шаг 3. Уменьшите или разрешите фракцию, если необходимо
Подобно операции сложения, при вычитании дробей вы все равно можете получить:
- Неправильная дробь, которую можно преобразовать в смешанное число
- Дробь, которую можно разрешить делением
- Дробь, которую можно упростить, найдя общий знаменатель
Часть 3 из 3: Нахождение общего знаменателя
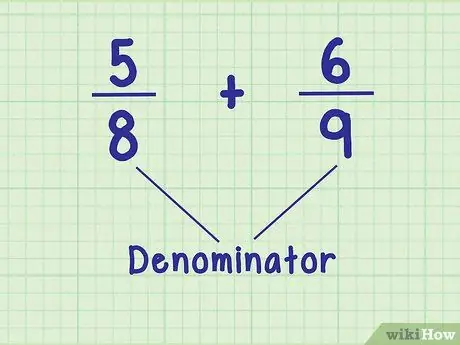
Шаг 1. Найдите знаменатели
У дробей не всегда одинаковые знаменатели, и чтобы их сложить или вычесть, необходимо найти общий знаменатель. Сначала найдите знаменатели рассматриваемых дробей.
Например, в уравнении 5/8 + 6/9 знаменатели 8 и 9

Шаг 2. Определите наименьшее общее кратное
Чтобы найти общий знаменатель, вам нужно найти наименьшее общее кратное двух чисел, то есть наименьшее положительное число, кратное двум исходным числам. Чтобы найти наименьшее общее кратное 8 и 9, вы должны сначала определить кратное каждого числа:
- Кратные 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104 и т. Д.
- Кратные 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108 и т. Д.
- Наименьшее общее кратное 8 и 9 равно 72.
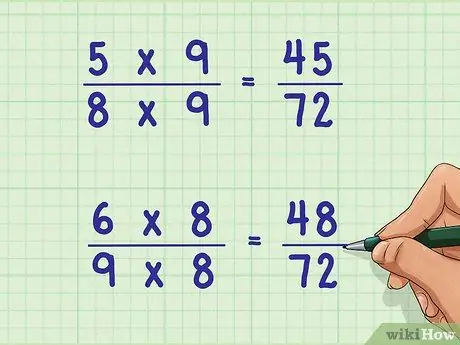
Шаг 3. Умножьте дроби, чтобы найти наименьшее общее кратное
Умножьте каждый знаменатель на правильное число, чтобы найти общий знаменатель. Помните, что все, что делается со знаменателем, должно выполняться и с числителем.
- В дроби 5/8: чтобы найти общий знаменатель 72, умножьте 8 x 9. Таким образом, вы должны умножить числитель на 9, то есть 5 x 9 = 45.
- В дроби 6/9: чтобы найти общий знаменатель 72, умножьте 9 x 8. Таким образом, вы должны умножить числитель на 8, то есть 6 x 8 = 48.

Шаг 4. Перепишите дроби
Новая дробь будет иметь общий знаменатель и произведение числителей, умноженных на те же значения:
- Фракция 5/8 будет преобразована в 45/72, а фракция 6/9 будет преобразована в 48/72.
- Теперь, когда у них есть общий знаменатель, вы можете сложить дроби 45/72 + 48/72 = 93/72.
- Не забывайте сокращать, решать или преобразовывать неправильную дробь в смешанное число, когда это возможно и необходимо.